Suppose we're given a 3 dimensional graph G, and we wish to check whether it is the boundary of a convex polyhedron. Armed with our definitions, we now have enough to explain how Melhorn et al check the convexity of polyhedrons.

So we're nearly there! We now have enough to be able to define a new way to test the convexity of a polyhedron.
A 3D simplicial polyhedron G is the surface of a convex polytope if and only if G is locally convex, and the projection of the seam of G is a globally convex polygon. The first direction makes sense, if G is globally convex, it will also be locally convex. In addition, the z-projection of the seam of a convex polyhedron will also be convex, and so will the projection of the seam of G. See the diagram in the definitions for a better idea of why this might be so.

Going the other way is a little bit more difficult, where we're trying to show that a polyhedron G which is locally convex, with a seam z-projection which is itself a convex polygon, is the surface bounding a convex polytope (a convex polyhedron). If we have that the z-projection of our seam, S'(G), is globally convex, then S(G) is nondegenerate. We can see this because were S(G) to be degenerate, we would have verticies with multiple edges emanating from them in the projection, which would clearly make S'(G) not globally convex.

We now take a point q' within the region defined by S'(G), and pass a vertical plane P through it. The intersection of P with the graph of G will be a closed curve on the plane of P, which will be locally convex, because by our first condition G is locally convex. Each 2-seam vertex of the curve will also correspond to a seam edge of G that is vertically projected to S'(G). Because P intersects with S'(G) at two edges or vertices, our new curve can have only two 2-seam vertices, if we remember our definitions, this means our curve must be a globally convex polygon. So a vertical line through the point q' intersects the curve only twice. If we take any point along the vertical line which is inside the curve Y, and call it q, if we rotate P around the vertical line, we can get infinitely many globally convex polygons, given by the intersection of the vertical plane and G. q will always be on the interior of the facets of G, so q is in the kernel of G.

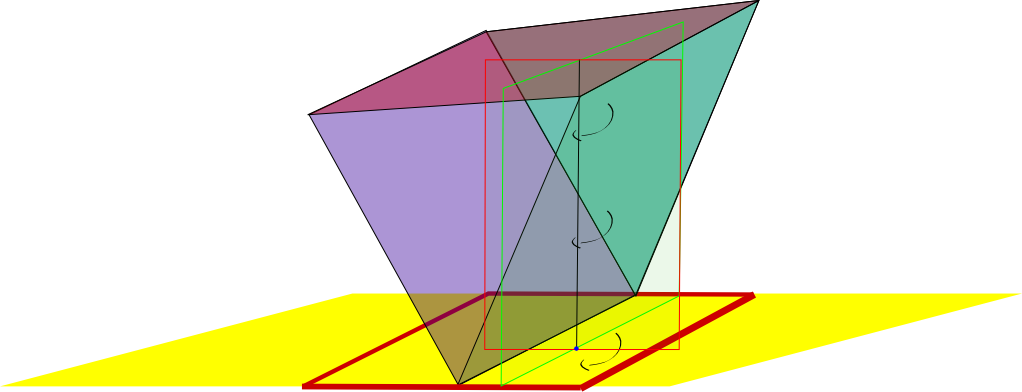
rayplane
If we take the blue point which is in the z-projection of the seam, in this case the red region on the yellow plane, and pass a vertical plane (notice we can rotate the plane 360 degrees around the point) through the point, the intersection of the polygon and the plane will be either a quadrilateral (for example with the green vertical plane) or a triangle (with the red vertical plane), both convex polygons themselves. We can see that every polygon on the plane will be convex for all


We can now see that G will be globally convex, if we consider q, and a non-vertical ray r from q, such that r intersects G only at facets of G. Say we take r', the z-projection of r. This ray r' will originate from point p', which will be interior to S'(G), the intersection of r' with the boundary of S'(G) will will be at k edges or vertices. Because S'(G) is globally convex, every ray coming from q' intersects S'(G) the same number of times. Using the result of Melholn et al, we know that r' will intsersect S'(G) at exactly one edge or vertex. So r will intersect G at exactly one facet. So the two conditions together work to define a globally convex polyhedron.

Having such a characterisation of a polygon is quite useful, and the purpose of the paper, an algorithm for checking the convexity of polyhedra, presents itself. The basic idea is to check for local convexity, and then to proceed to check the 2-seam of the z-projection of the seam for convexity, it does this by ensuring there is only one rightmost 2-seam vertex (remember that a convex polygon will have only two vertices in its 2-seam), if there is more than one rightmost vertex in the 2-seam, the projection is not convex, and thus the graph G is not the boundary of a convex polytope. A summary of the algorithm is as follows:

For each edge e in the graph:
   If e is not locally convex, we return false.
   If e is a seam edge, we let u and v be the endpoints of e. If v already has two seam edges incident on it, we return false, because a vertex with 3 seam edges makes the seam of G degenerate, which accordingly makes G non-convex. We then increment the count of seam edges incident on v, and set p(v) to be u. If the count of edges incident on v was already 1, we check if v is a right-2-seam vertex, by checking p(v) and u (which are the two vertices connected to v by the seam edges), if it is a right-2-seam vertex, we see if we have already found such a vertex, if we have, we return false, if we haven't, we make note that we have.
If we can proceed through all edges of G without returning false, then we can conclude that G is the boundary of a convex polytope.
The check-3-polytope algorithm as presented by O Devillers. et al.

The general idea of the algorithm can be summarised as follows: we're checking whether the polyhedron is locally convex at every edge, and we're also checking if the projection of the seam edges is convex, by ensuring it has only one right-most point. Pretty elegant!

Interestingly, a similar idea to this can be applied to d-dimensional spaces. The only difference is that we recursively project the seam of the graph until we reach our 3D case, for example, we project the seam of our original graph G, which has dimension d, to dimension d-1, this projection we then again take the projection of its seam to dimension d-2, and so on, until we reach our base case where the dimension is three. We then check, as above, whether the 2-seam is globally convex. This procedure is also linear in the number of vertices/edges. Details can be found in the paper given in the references.

This algorithm runs in linear time with respect to the number of edges of G, as we visit each edge only once, so this checker is optimal! However, it does rely on a very specific input, in the paper, the input is a 3D graph as well as an ordering of the graph, which allows the algorithm to easily tell which facets are interior and which are exterior, which in turn is very useful for determining whether edges are seam edges as well as whether they're locally convex. This is however very difficult to input correctly.

An implementation of the algorithm below should give you an idea of how the algorithm works. To select a point, click on it, to add an edge between points, select one point, then while holding the Ctrl key, select another point.

For each edge you add, you'll also need to specify the facets which are incident to the edge by first selecting the edge, you do this by selecting the first vertex in the edge, then holding the Ctrl key and selecting the other vertex in the edge. The edge should highlight in blue, at this point, you select the two facets incident on the edge by selecting holding down the Shift key and selecting the points that make the facets, the other edges that make up the facet should turn purple. At this point it will also draw the normal using a yellow line. The yellow line of the facet must point to the INTERIOR of the polyhedron.

A good way of quickly moving between the edges you need to add facets to is to press C to ask it to check the convexity, and then add the facets for the edge the applet highlights. The seam edges of the graph will be highlighted in green for you, and the applet should also be able to tell you whether your polygon is globally convex or not. Occasionally the applet seems to be unable to regain the focus sometimes if you switch windows, so if the keys seem not to work, reloading the page is your best bet. More details about why an edge may or may not be a seam edge can be found if you open a Java console window (generally by right clicking in the applet window or at the bottom of your browser) and view the output there. The source code can be found on my homepage at http://www.cs.mcgill.ca/~tflook/.

Key summary: